求定義域的方法:整式的定義域為R。整式可以分為單項式還有多項式,單項式比如y=4x,多項式比如y=4x+1。這時候無論是單項式還是多項式,定義域均為{x|x∈R},就是x可以等于所有實數(shù)。分式的定義域是分母不等于0。

①整式的定義域為R。整式可以分為單項式還有多項式,單項式比如y=4x,多項式比如y=4x+1。這時候無論是單項式還是多項式,定義域均為{x|x∈R},就是x可以等于所有實數(shù)。
②分式的定義域是分母不等于0。例如y=1/(x-1),這時候的定義域只需要求讓分母不等于即可,即x-1≠0,定義域為{x|x≠1}。
③偶數(shù)次方根定義域是被開方數(shù)≥0。例如根號下x-3,這時候定義域就是讓x-3≥0,求出來定義域為{x|x≥3}。
④奇數(shù)次方根定義域是R。例如三次根號下x-3,定義域就是{x|x∈R}。
⑤指數(shù)函數(shù)定義域為R。比如y=3^x,定義域為{x|x∈R}。
⑥對數(shù)函數(shù)定義域為真數(shù)>0。比如log以3為底(x-1)的對數(shù),讓x-1>0,即定義域為{x|x>1}。
⑦冪函數(shù)定義域是底數(shù)≠0。比如y=(x-1)^2,讓x-1≠0,即定義域為{x|x≠1}。
⑧三角函數(shù)中正弦余弦定義域為R,正切函數(shù)定義域為x≠π/2+kπ。這時候求定義域畫個圖就可以看出來了,只要記住三角函數(shù)圖像,即可求出定義域。
定義一:設(shè)x、y是兩個變量,變量x的變化范圍為D,如果對于每一個數(shù)x∈D,變量y遵照一定的法則總有確定的數(shù)值與之對應(yīng),則稱y是x的函數(shù),記作y=f(x),x∈D,x稱為自變量,y稱為因變量,數(shù)集D稱為這個函數(shù)的定義域。
定義二:A,B是兩個非空數(shù)集,從集合A到集合B 的一個映射,叫做從集合A到集合B 的一個函數(shù)。記作 或 其中A就叫做定義域。通常,用字母D表示。通常定義域是F(X)中x的取值范圍。

檢驗鐵離子的方法:加入氫氧化鈉溶液,生成白色沉淀,白色沉淀迅速變成灰綠色,最后,變成紅褐色,這證明有鐵離子。向溶液中加入酸性高錳酸鉀,若褪色...
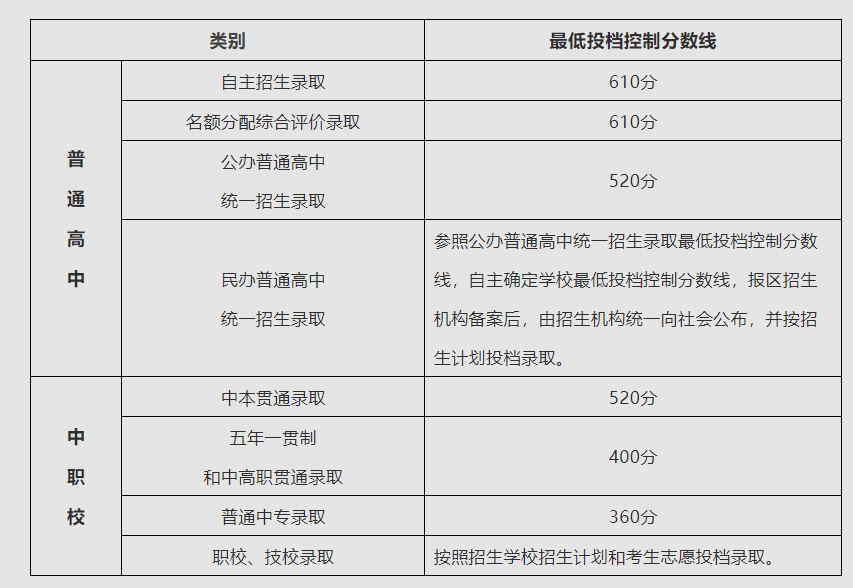
預(yù)計2023年上海各高中中考分?jǐn)?shù)線在500-650分之間,由于中考還未開始,請參考2022年上海高中錄取分?jǐn)?shù)線:公辦普通高中分?jǐn)?shù)線實在520...

函數(shù)線性相關(guān)與無關(guān)的判斷方法:確定函數(shù)線性相關(guān)性有若干判斷方法,其中一種是經(jīng)驗判別法。在這種判定方 法中,研究者根據(jù)自變量和因變量的實際情況...

氧化性還原性強弱比較方法:一般來說元素的最高價只有氧化性,最低價只有還原性,中間的既有氧化性又有還原性。對金屬來說:越活潑單質(zhì)的還原性越強,...

梯形中位線證明方法:第一種方法是做輔助線,然后利用三角形相似定理進行證明。第二種方法也是做輔助線,用的是向量法進行證明的。梯形中位線定理是幾...

在直角三角形中,兩直角邊的平方和等于斜邊的平方,即:勾2+股2=弦2,32+42=52。“勾三股四弦五”是勾股定理的一個特別的例子,由西周初...

2023年高考261分能上新疆科技學(xué)院、甘肅交通職業(yè)技術(shù)學(xué)院、河北軟件職業(yè)技術(shù)學(xué)院、吉林司法警官職業(yè)學(xué)院、江西交通職業(yè)技術(shù)學(xué)院、云南醫(yī)藥健康...

2023年高考260分能上宿州職業(yè)技術(shù)學(xué)院、湖北城市建設(shè)職業(yè)技術(shù)學(xué)院、江西應(yīng)用技術(shù)職業(yè)學(xué)院、江陰職業(yè)技術(shù)學(xué)院、長江工程職業(yè)技術(shù)學(xué)院、重慶公共...